Bài Tập Môn Toán Rời Rạc

Đề Bài

Trình bày tóm tắt và cài đặt bài toán “Người du lịch”

Người thực hiện:   Nguyễn Mạnh Cường  MSV:1400088

                               Lê Thái Hòa                  MSV:1400133

                               Nhữ Công Vụ             MSV:1400132

Giảng Viên: Trần Xuân Thanh

Mục lục

Giới thiệu :

Chương I : Bài toán người du lịch và các thuật giải

1      Giới thiệu lịch sử của bài toán người du lịch

2      Mô tả chi tiết bài toán

3     Thuật giải chính xác

4      Thuật giải gần đúng (Heuristic)

     4.1 Thuật giải tham lam (thuật giải láng giềng gần nhất)

     4.2  Thuật giải nhánh cận

1/Giới thiệu về lịch sử của bài toán người du lịch

    Bài toán người du lịch là một vẫn đề kết nối tối ưu trong nghiên cứu khoa học máy tính. Cho một danh sách các thành phố và các cặp khoảng cách giữa 2 thành phố trong đó, nhiệm vụ là phỉa tìm một chu trình ngắn nhất để thăm mỗi thành phố một lần duy nhất.

   Trong hình trên, tour để người du lịch có thể thăm hết tất cả các thành phố với chi phí ngắn nhất được thể hiện bằng các cạnh màu đỏ.

   Vấn đề này được nêu ra lần đầu tiên như là một vấn đề toán học vào năm 1930 và là vấn đề được tập trung nghiên cứu nhiều nhất trong lĩnh vực tối ưu. Nó được sử dụng thử nghiệm, đánh giá các thuật toán tối ưu. Tuy vấn đề có tính phức tạp cao, nhưng có rất nhiều phương pháp chính xác và gần đúng đã được biết đến, do đó có thể giải được vài trường hợp có đến 10 ngàn thành phố.

   Trong những năm 1950 và 1960, bài toán trở nên phổ biến trong giới khoa học châu Âu và ở Mỹ. Các công trình đáng kể đầu tiên được thực hiện bởi Georgeo Dantzig, Delbert ray Fulkerson và Selmer M.Johnson người đã đề xuất bài toán như một chương trình tuyến tính và phát triển phương pháp nhánh cận cho bài toán. Với các phương pháp mới họ đã giải một trường hợp với 49 thành phố một các tối ưu bằng cách xây một chu trình và chứng minh rằng không có chu trình nào ngắn hơn. Trong nhiều thập kỉ sau đó, bài toán được nghiên cứu trong rất nhiều ngành như toán học, khoa học máy tính, hóa học, vật lý.

2/Mô tả chi tiết bài toán

     Bài toán người du lịch có thể biểu diễn thành một đồ thị, trong đó các thành phố là các đỉnh, các con đường đi lại giữa các thành phố là các cạnh, đồng thời khoảng cách giữa các thành phố là trọng số tương ứng của cạnh nối chúng. Tất nhiên, đồ thị sau khi xây dựng xong là đồ thị đủ, giữa hai thành phố không có đường đi trực tiếp mà phải thông qua một thành phố khác thì ta gán trọng số của cạnh đó số lớn nhất có thể. Khi đóm bài toán người du lịch trở thành bài tìm một chu trình Hamilton ngắn nhất, và lộ trình của người du lịc chính là chu trình hamilton ngắn nhất.

      Nếu như khoảng cách giữa hai thành phố bất ki là như nhau cho cả hai hướng thi dùng đồ thị vô hướng, ngược lại là sử dụng đồ thị có hướng. Trong ví dụ trên, ta giả định đường đi từ 2 hướng là như nhau.

      Trường hợp khoảng cách giữa các thành phố trong đồ thị là khoảng cách metric ( tức là thỏa bất đẳng thức tam giác Cij <= Cik + Ckj), thì khoảng cách trực tiếp từ thành phố A đến thành phố B là khoảng cách ngắn nhất và không bao giờ lớn hơn khoảng cách mà có thông qua thành phố C. Thực tế, khi các thành phố được biểu diễn bởi các điểm trên mặt phẳng, rất nhiều các khoảng cách gần như là khoảng cách metric.

      Trong nhiều trường hợp, các khoảng cách không thỏa bất đẳng thức tam giác hoặc do tiêu chí đánh giá khoảng cách không thuộc không gian metric chẳng hạn như khoảng cách theo tiêu chí thời gian di chuyển, rõ ràng máy bay di chuyển nhanh hơn nhiều so với ô tô mặc dù khoảnh cách di chuyển có thể lớn hơn.

3/Thuật toán chính xác

     Trong các thuật toán chính xác cho bài toán người du lịch, đầu tiên phải kể đến thuật toán vét cạn. Thuật toán này tìm tất cả cách chu trình Hamilton được thực hiện theo phương pháp duyệt chiều sâu và kết hợp quay lui. Do quá trình duyệt có thể rất sâu nên ta không sử dụng đệ quy mà dùng stack để khử đệ quy. Sử dụng một biến min để lưu lại tổng trọng số của chu trình Hamilton nhỏ nhất. Ban đầu  min=+∞ hoặc min= m* trọng số của cạnh lớn nhất.

     Chu trình Hamilton là chu trình đi qua hết tất cả các đỉnh và sau đó quay về đỉnh xuất phát, do đó, ta dùng một danh sách ChuaXet[] để lưu lại các đỉnh chưa xét, một biến Sum để lưu lại trọng số của chu trình hiện thời, do chu trình hamilton không quan trọng đỉnh xuất ohats, ta chọn đỉnh xuất phát là đỉnh có chỉ số nhỏ nhất là 1.

Quá trình duyệt như sau:

     -Ban đầu đưa đỉnh 1 và 0 vào stack, Sum = 0.

     -Lặp lại quá trình sau: Lấy (Top) đỉnh từ stack ra là đỉnh i và trọng số ts, gán ChuaDuyet[i] là false và Sum+=ts, nạp 0 0 vào stack sau đó nạp các đỉnh kề j và trọng số tương ứng với đỉnh đang xét mà ChuaDuyet[j]=true, nếu i không có đỉnh kề thỏa yêu cầu, tức là đã duyệt hết tất cả các đỉnh ( do đồ thị đang xé là đồ thị đủ). ta cộng trọng số của cạnh i>1 vào Sum và gán min bằng Min(Sum,min). Sum- = cạnh i>1. Lặp lại quá trình sau: Lấy đỉnh từ stack ra, nếu đỉnh này không còn đỉnh kề thỏa yêu cầu thì Pop đỉnh và trọng số này ra, nếu có đỉnh thỏa thì vòng lặp và duyệt tiếp từ đỉnh này, trường ợp lấy đỉnh từ stack ra là 0 thì Pop 2 lần để lấy 2 đỉnh liên tục trong stack ra sau đó tiếp tục vòng lặp.

4/Các thuật giải gần đúng (Heuristic)

4.1/ Thuật giải tham lam ( thuật giải láng giếng gần nhất)

   Thuật giải vét cạn ở trên cho ta một đáp án tối ưu, tuy nhiên độ phức tạp của nó là quá cao(n-1)!thuộc nhóm O(n!). Do đó, trong thực tiễn người ta chấp nhận các thuật giải cho kết quả tốt ( nhưng không phải lúc nào củng tốt) bởi sự đơn giản, nhanh chóng và cài đặt dễ dàng. Một trong các thuật giải đó là thuật giải tham lam hay còn gọi là thuật toán láng giềng gần nhất. Trong thuật toán này, tạo mỗi bước, ta chọn con đường (cạnh) nối với các thành phố ( đỉnh) gần nhất với hy vọng rằng n con đường ngắn nhất sẽ cho ra đường đi ngắn nhất.

Ví dụ sau đây minh họa cho thuật toán giải tham lam với n=5

   

4.2/ Thuật toán nhánh cận

      Thuật toán nhánh cận là phương pháp chủ yếu để giải các bài toán tối ưu tổ hợp. Tư tưởng cơ bản của thuật toán là trong quá trình tìm kiếm lời giải, ta sẽ phan hoạch tập hợp các phương án thành hai hay nhiều nhánh con như cây tìm kiếm, sau đó đánh giá từng nhánh để quyết định xem nên tiếp tục ở nhanh nào và loại bỏ nhánh nào mà các phương án con của nó không thể là phương án tối ưu.

      trong thuật toán trình bày dưới đây, chúng ta sẽ tìm kiếm lời giải dựa trên ma trận trọng số C[][]. Đối với bài toán người du lịch, khi tiến hành tìm kiếm lời giải chúng ta sẽ ohaan tập các hành trình thành 2 tập con: Tập gồm những hành trình có chứa cạnh (i,j) và tập còn lại gồm những hành trình không chứa cạnh (i,j).

Trước tiên, để cho việc phân nhánh được dễ dàng, ta cần phải rút gọn ma trận trọng số, đó tổng chi phí của hành trình sẽ chứa đúng một phần tử của mỗi dòng và mỗi cột nên khi cộng hay trừ cả dòng hay cột cho một số α thì tổng trọng số của tất cả các hành trình sẽ giảm đi α.Do đó, ta có thể rút gọn ma trận trọng số sao cho trên mỗi dòng và cột đều có ít nhất một số 0, đồng thời, tổng của các số α sẽ là cận dưới của tất cả các hành trình.

        Đối với tập phân hoạch chứa cạnh i,j. Do i,j thuộc hành trình này nên ta phái xóa dòng i cột j do khong thể có cạnh khác từ i đi ra và từ j đi vào ngoài cạnh i,j. ngoài ra cũng đặt C[j][i] bằng ∞ do đã chọn cạnh C[i][j].

Đối với tập phân hoạch không chứa cạnh i,j là lớn nhất, để tìm cạnh đó ta chọn số 0 trong ma trận để thay nó bằng ∞ sẽ cho ta tổng hằng số rút gọn theo cạnh và dòng lớn nhất.

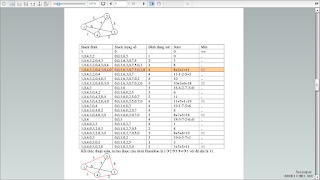
Ví dụ: giải bài toán người du lịch với ma trận chi phí như sau: